Цепи Маркова
Цепи Маркова
Орграфы возникают во многих жизненных ситуациях. Не пытаясь охватить
большое число таких ситуаций, ограничимся рассмотрением одной из них.
Интересующихся данными приложениями отошлем к главе  книги
Басакера и Саати "Конечные графы и сети".М.: Наука. 1974.
книги
Басакера и Саати "Конечные графы и сети".М.: Наука. 1974.
Задача, которую мы рассмотрим, интересна сама по себе, а отчасти рассматриваем мы ее из-за того, что ее изложение не требует введения большого количества новых терминов.
Рассмотрим задачу об осле, стоящем точно между двумя копнами: соломы ржи и соломы пшеницы (рис. 10.5).
Осел стоит между двумя копнами: "Рожь" и "Пшеница"
(рис. 10.5). Каждую минуту он либо передвигается на десять метров в сторону первой копны
(с вероятностью 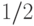 ), либо в сторону второй копны (с
вероятностью
), либо в сторону второй копны (с
вероятностью 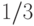 ), либо остается там, где стоял (с вероятностью
), либо остается там, где стоял (с вероятностью 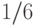 ); такое поведение называется одномерным случайным блужданием. Будем
предполагать, что обе копны являются "поглощающими" в том смысле,
что если осел подойдет к одной из копен, то он там и останется. Зная
расстояние между двумя копнами и начальное положение осла, можно поставить
несколько вопросов, например: у какой копны он очутится с большей
вероятностью и какое наиболее вероятное время ему понадобится, чтобы
попасть туда?
); такое поведение называется одномерным случайным блужданием. Будем
предполагать, что обе копны являются "поглощающими" в том смысле,
что если осел подойдет к одной из копен, то он там и останется. Зная
расстояние между двумя копнами и начальное положение осла, можно поставить
несколько вопросов, например: у какой копны он очутится с большей
вероятностью и какое наиболее вероятное время ему понадобится, чтобы
попасть туда?
Чтобы исследовать эту задачу подробнее, предположим, что расстояние между
копнами равно пятидесяти метрам и что наш осел находится в двадцати метрах
от копны "Пшеницы". Если места, где можно остановиться, обозначить
через 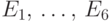 (
(  — сами
копны), то его начальное положение
— сами
копны), то его начальное положение 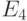 можно задать вектором
можно задать вектором 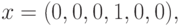
 -я
компонента которого равна вероятности того, что он первоначально находится
в
-я
компонента которого равна вероятности того, что он первоначально находится
в 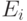 . Далее, по прошествии одной минуты вероятности его
местоположения описываются вектором
. Далее, по прошествии одной минуты вероятности его
местоположения описываются вектором 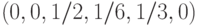 , а через
две минуты — вектором
, а через
две минуты — вектором 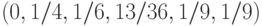 . Ясно, что
непосредственное вычисление вероятности его нахождения в заданном месте по
прошествии
. Ясно, что
непосредственное вычисление вероятности его нахождения в заданном месте по
прошествии  минут становится затруднительным. Оказалось, что
удобнее всего ввести для этого матрицу перехода.
минут становится затруднительным. Оказалось, что
удобнее всего ввести для этого матрицу перехода.
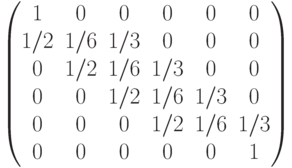
Пусть 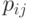 — вероятность того, что он переместится
из
— вероятность того, что он переместится
из 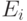 в
в 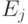 за одну минуту. Например,
за одну минуту. Например,  и
и 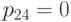 .
Эти вероятности
.
Эти вероятности 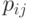 называются вероятностями перехода,
а
называются вероятностями перехода,
а  -матрицу
-матрицу 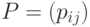 называют матрицей
перехода. Заметим, что каждый элемент
матрицы
называют матрицей
перехода. Заметим, что каждый элемент
матрицы  неотрицателен и что сумма элементов любой из строк равна единице. Из всего
этого следует, что
неотрицателен и что сумма элементов любой из строк равна единице. Из всего
этого следует, что  — начальный вектор-строка,
определенный выше, местоположение осла по прошествии одной минуты описывается
вектором-строкой
— начальный вектор-строка,
определенный выше, местоположение осла по прошествии одной минуты описывается
вектором-строкой 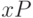 , а после
, а после  минут —
вектором
минут —
вектором 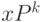 . Другими
словами,
. Другими
словами,  -я компонента вектора
-я компонента вектора 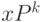 определяет
вероятность того,
что по истечении
определяет
вероятность того,
что по истечении  минут осел оказался в
минут осел оказался в 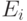 .
.
Можно обобщить эти понятия. Назовем вектором вероятностей
вектор-строку, все компоненты которого неотрицательны и дают в сумме
единицу. Тогда матрица перехода определяется как квадратная
матрица, в которой каждая строка является вектором вероятностей. Теперь
можно определить цепь Маркова (или просто цепь) как пару 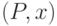 ,
где
,
где  есть
есть  -матрица перехода, а
-матрица перехода, а  есть
есть 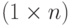 -вектор-строка. Если каждый элемент
-вектор-строка. Если каждый элемент 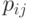 из
из  рассматривать как
вероятность перехода из позиции
рассматривать как
вероятность перехода из позиции 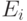 в позицию
в позицию 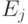 , а
, а  — как
начальный вектор вероятностей, то придем к классическому понятию дискретной стационарной цепи Маркова, которое можно найти в книгах
по теории вероятностей (см. Феллер В. Введение в теорию вероятностей и ее
приложения. Т.1. М.: Мир. 1967) Позиция
— как
начальный вектор вероятностей, то придем к классическому понятию дискретной стационарной цепи Маркова, которое можно найти в книгах
по теории вероятностей (см. Феллер В. Введение в теорию вероятностей и ее
приложения. Т.1. М.: Мир. 1967) Позиция 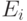 обычно называется состоянием
цепи. Опишем различные способы их классификации.
обычно называется состоянием
цепи. Опишем различные способы их классификации.
Нас будет интересовать следующее: можно ли попасть из одного данного
состояния в другое, и если да, то за какое наименьшее время. Например, в
задаче об осле из 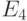 в
в 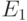 можно попасть за
три минуты и вообще нельзя попасть из
можно попасть за
три минуты и вообще нельзя попасть из 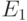 в
в 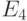 . Следовательно,
в основном мы будем интересоваться не самими вероятностями
. Следовательно,
в основном мы будем интересоваться не самими вероятностями 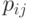 , а тем,
положительны они или нет. Тогда появляется надежда, что все эти данные удастся представить
в виде орграфа, вершины которого соответствуют состояниям, а дуги
указывают на то, можно ли перейти из одного состояния в другое за одну
минуту. Более точно, если каждое состояние
, а тем,
положительны они или нет. Тогда появляется надежда, что все эти данные удастся представить
в виде орграфа, вершины которого соответствуют состояниям, а дуги
указывают на то, можно ли перейти из одного состояния в другое за одну
минуту. Более точно, если каждое состояние 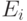 представлено
соответствующей ему вершиной
представлено
соответствующей ему вершиной 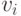 , то, проводя
из
, то, проводя
из 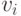 в
в 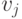 для тех и только тех вершин, для которых
для тех и только тех вершин, для которых  , мы и
получим требуемый орграф. Кроме того, этот орграф можно определить при помощи его
матрицы смежности, если заменить каждый ненулевой элемент
матрицы
, мы и
получим требуемый орграф. Кроме того, этот орграф можно определить при помощи его
матрицы смежности, если заменить каждый ненулевой элемент
матрицы  на
единицу. Мы будем называть этот орграф ассоциированным орграфом
данной цепи Маркова. Ассоциированный орграф одномерного случайного
блуждания, связанного с задачей об осле, изображен на (рис. 10.7).
на
единицу. Мы будем называть этот орграф ассоциированным орграфом
данной цепи Маркова. Ассоциированный орграф одномерного случайного
блуждания, связанного с задачей об осле, изображен на (рис. 10.7).


